But what is interleaving?! - Part 2
- Amarbeer Singh Gill

- Jul 19, 2022
- 5 min read
One of the strategies I explore in my book is interleaving. In part 1 we set the scene for how my thinking around interleaving has developed by looking at my original thinking and how I'd missed the mark. In this part we'll look at why my original thinking was flawed and how it has developed since.
Why interleaving is more than just "mixing"
Let's briefly recap my initial attempt at interleaving:
"I was working on probability trees with year 9, but having covered Pythagoras' theorem a few weeks prior had mixed a few questions to do with that between my slides on probability trees - I'd interleaved! (Spoiler alert: I definitely hadn't)."
I believed I'd interleaved because I'd only focused on the surface feature of interleaving - mixing related things up (in this case the relation was they were both "maths"). But understanding more about how our brain works led me to believe I'd missed the mark, and by quite some distance!
Cognitive Load
Some of the key findings of cognitive load theory (CLT) is that working memory (WM):
has a very limited capacity and can only handle about 4 "chunks" of information
struggles retain information over any period of time longer than a few minutes
The size of those chunks however can vary dramatically when our long-term memory (LTM) kicks in to support us. For example, "CAT" will be one chunk of information for people reading this blog because the collection of letters has meaning for us, but to a young child learning to read each letter would count as a chunk. Because the learning is new and they haven't associated any meaning to the collection of letters they can't get any support from their LTM and so their WM is working significantly harder than if they were able to process it as one word. In the example from my classroom I was teaching students about probability trees. This information was new and so they didn't have relevant knowledge in their LTM to help them make meaning of the new learning, which would have supported their WM in its processing.
Why is this relevant to interleaving? Because alongside not receiving much support from their LTM, I'd placed gaps between problems with learning that was completely unrelated (the Pythagoras questions). So we end up with a perfect storm of WM overload:
Little to no knowledge in LTM to support processing of new learning
Attention being split between unrelated topics
Gaps between probability tree questions (new learning) was having to be retained mostly in WM, which only has a capacity of a few minutes at most
So it was no surprise that they struggled to come back and answer the probability tree questions - their attention had been split so by the time we got back they'd lost most of their thinking around probability trees. Instead of supporting their learning it's more than likely my teaching had just confused them.
A Better Attempt
The key mistake I'd made above was not being granular enough about how related my topics were. I'd misplaced my focus on the surface features and the "how" of interleaving and had not taken the time to understand why interleaving should work.
There appear to be several key features to what makes interleaving successful:
Concepts must be closely related
This assists in students drawing comparisons between concepts.
The similarities and differences must be explicitly discussed
Students must have clarity of what differentiates one concept from another and how they relate.
The interleaving must occur at the same time (i.e. the two concepts are being compared together, rather than one being taught and then the second taught later and students are asked to compare).
This will avoid attention being split for too long a period of time.
Let's look at a concrete example: radius and diameter.
Blocked Practice
(Interleaved practice stands in contrast to blocked practice. In blocked practice, students will study concept before moving on to a different one, and a different one etc.)
In blocked practice, I'd most likely just show students what the radius is on a diagram, its relationship with diameter, and then give several questions getting students to state the diameter and radius when given a radius. I'd then do similar for diameter so the practice would look like this:
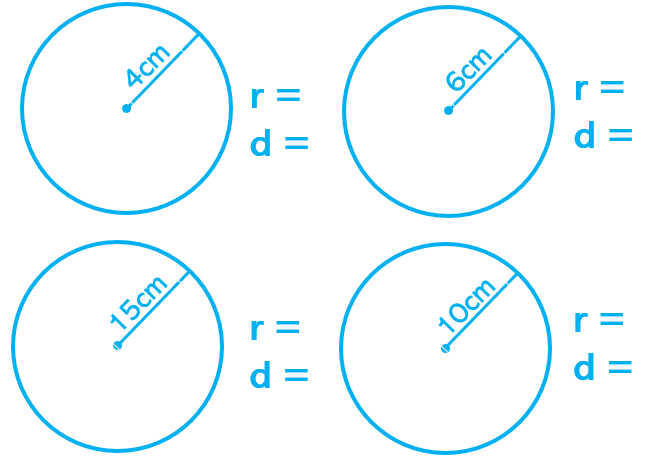

In each of these cases, students would likely not have to think very hard about what property (radius/diameter) they're given to start with as they can just know from the question which type it is. This would mean not having to think particularly hard about the relationship, but instead all they need to do is double/halve the numbers as appropriate.
Interleaved Practice
When interleaving though, I'd teach both radius and diameter, and the relationship between them, at the same time. So the practice in this instance would look like this:
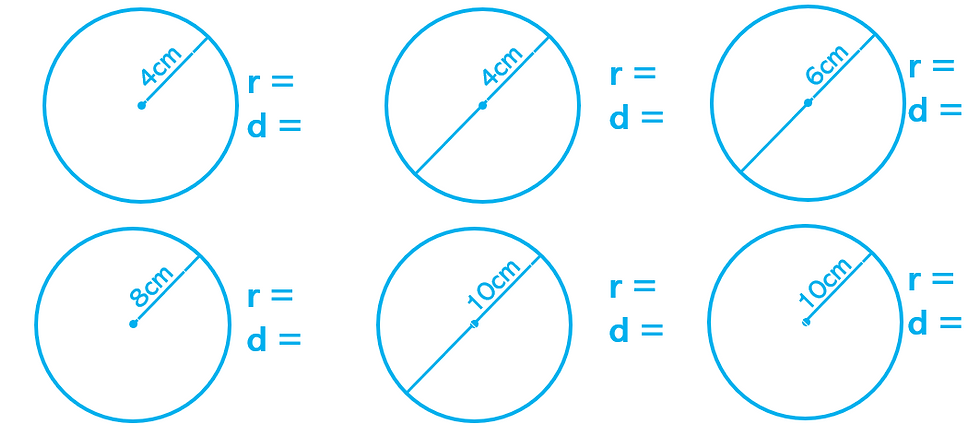
For these questions students students will first need to figure out what property they've been given as well as how that relates to the missing property.
Why can this be better?
Firstly, students are given exponentially more opportunities to retrieve the correct learning in the interleaved practice and the benefits of retrieval have been discussed widely. For each question they would have to retrieve:
What is radius/diameter?
Which one is in the diagram?
What is the relationship between radius & diameter?
Now that I've got one of them, how do I work out the other one?
Students are having to think hard about each and every question, which plays into the second potential mechanism at work: highlighting underlying structures. Students can't just assume that they have a particular measurement because that's what the questions before had, they have to identify it using the underlying characteristics of the concepts. This leads into another mechanism: strengthening of cue-memory relationships. Each time students are forced to go link the diagram they're looking at to the definitions of the concepts from memory, they're strengthening how well that same cue will act as a trigger for that memory the next time they see it.
Because the concepts are related we avoid splitting attention over too long a period of time (a pitfall of my previous practice). Students aren't having to switch their attention back and forth between unrelated chunks as instead of it being seen as two different chunks (radius and diameter), we are facilitating the creation of one larger chunk (properties of a circle). So whilst they may not be receiving much support from LTM, their WM is better equipped to handle the processing.
So in summary, interleaving works because:
Students are forced to analyse similarities and differences between related concepts.
This forces students to keep in mind underlying structures when working through problems.
Which strengthens the relationship between the cue (from the question) and the memory (the underlying structure), so students are able to identify it more easily in future.
All of this multiplies opportunities for retrieval of those ideas, strengthening those memories in the process also.
N.B. This does not mean that radius and diameter should always be taught as above. The prior knowledge of our students, their current abilities and a whole host of other factors should determine at what point in the learning introducing this might be appropriate, and how much scaffolding they might need before getting to that point.



Comments